Fuzzy measure theory
Fuzzy measure theory considers a number of special classes of measures, each of which is characterized by a special property. Some of the measures used in this theory are plausibility and belief measures, fuzzy set membership function and the classical probability measures. In the fuzzy measure theory, the conditions are precise, but the information about an element alone is insufficient to determine which special classes of measure should be used. The central concept of fuzzy measure theory is the fuzzy measure (also capacity, see [1]) which was introduced by Choquet in 1953 and independently defined by Sugeno in 1974 in the context of fuzzy integrals.
Contents |
Axioms
Fuzzy measure can be considered as generalization of the classical probability measure. A fuzzy measure g over a set X (the universe of discourse with the subsets E, F, ...) satisfies the following conditions:
A fuzzy measure g is called normalized if 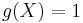 .
.
Properties of fuzzy measures
For any 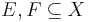 , a fuzzy measure is:
, a fuzzy measure is:
- additive if
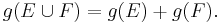 for all
for all 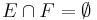 ;
; - supermodular if
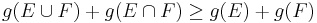 ;
; - submodular if
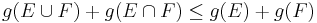 ;
; - superadditive if
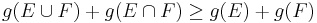 for all
for all 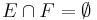 ;
; - subadditive if
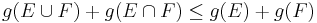 for all
for all 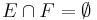 ;
; - symmetric if
 implies
implies  ;
; - Boolean if
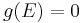 or
or 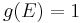 .
.
Understanding the properties of fuzzy measures is useful in application. When a fuzzy measure is used to define a function such as the Sugeno integral or Choquet integral, these properties will be crucial in understanding the function's behavior. For instance, the Choquet integral with respect to an additive fuzzy measure reduces to the Lebesgue integral. In discrete cases, a symmetric fuzzy measure will result in the ordered weighted averaging (OWA) operator. Submodular fuzzy measures result in convex functions, while supermodular fuzzy measures result in concave functions when used to define a Choquet integral.
Möbius representation
Let g be a fuzzy measure, the Möbius representation of g is given by the set function M, where for every 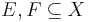 ,
,
The equivalent axioms in Möbius representation are:
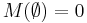 .
.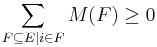 , for all
, for all 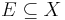 and all
and all 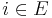
A fuzzy measure in Möbius representation M is called normalized if 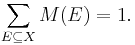
Möbius representation can be used to give an indication of which subsets of X interact with one another. For instance, an additive fuzzy measure has Möbius values all equal to zero except for singletons. The fuzzy measure g in standard representation can be recovered from the Möbius form using the Zeta transform:
Simplification assumptions for fuzzy measures
Since fuzzy measures are defined on the power set (or, more formally, on the sigma algebra associated with  ), even in discrete cases the number of variables can be quite high (
), even in discrete cases the number of variables can be quite high (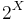 ). For this reason, in the context of multi-criteria decision analysis and other disciplines, simplification assumptions on the fuzzy measure have been introduced so that it is less computationally expensive to determine and use. For instance, when it is assumed the fuzzy measure is additive, it will hold that
). For this reason, in the context of multi-criteria decision analysis and other disciplines, simplification assumptions on the fuzzy measure have been introduced so that it is less computationally expensive to determine and use. For instance, when it is assumed the fuzzy measure is additive, it will hold that 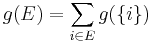 and the values of the fuzzy measure can be evaluated from the values on X. Similarly, a symmetric fuzzy measure is defined uniquely by |X| values. Two important fuzzy measures that can be used are the Sugeno- or
and the values of the fuzzy measure can be evaluated from the values on X. Similarly, a symmetric fuzzy measure is defined uniquely by |X| values. Two important fuzzy measures that can be used are the Sugeno- or  -fuzzy measure and k-additive measures, introduced by Sugeno[2] and Grabisch[3] respectively.
-fuzzy measure and k-additive measures, introduced by Sugeno[2] and Grabisch[3] respectively.
Sugeno  -measure
-measure
The Sugeno  -measure is a special case of fuzzy measures defined iteratively. It has the following definition:
-measure is a special case of fuzzy measures defined iteratively. It has the following definition:
Definition
Let 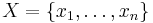 be a finite set and let
be a finite set and let 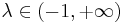 . A Sugeno
. A Sugeno  -measure is a function g from
-measure is a function g from 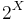 to [0, 1] with properties:
to [0, 1] with properties:
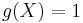 .
.- if
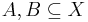 (alternatively
(alternatively 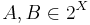 ) with
) with 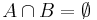 then
then 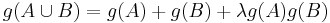 .
.
As a convention, the value of g at a singleton set 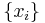 is called a density and is denoted by
is called a density and is denoted by 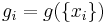 . In addition, we have that
. In addition, we have that  satisfies the property
satisfies the property
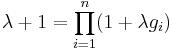 .
.
Tahani and Keller [4] as well as Wang and Klir have showed that once the densities are known, it is possible to use the previous polynomial to obtain the values of  uniquely.
uniquely.
k-additive fuzzy measure
The k-additive fuzzy measure limits the interaction between the subsets 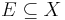 to size
to size 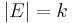 . This drastically reduces the number of variables needed to define the fuzzy measure, and as k can be anything from 1 (in which case the fuzzy measure is additive) to
. This drastically reduces the number of variables needed to define the fuzzy measure, and as k can be anything from 1 (in which case the fuzzy measure is additive) to 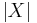 , it allows for a compromise between modelling ability and simplicity.
, it allows for a compromise between modelling ability and simplicity.
Definition
A discrete fuzzy measure g on a set X is called k-additive (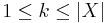 ) if its Möbius representation verifies
) if its Möbius representation verifies 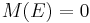 , whenever
, whenever 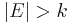 for any
for any 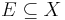 , and there exists a subset F with k elements such that
, and there exists a subset F with k elements such that 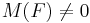 .
.
Shapley and interaction indices
In game theory, the Shapley value or Shapley index is used to indicate the weight of a game. Shapley values can calculated for fuzzy measures in order to give some indication of the importance of each singleton. In the case of additive fuzzy measures, the Shapley value will be the same as each singleton.
For a given fuzzy measure g, and 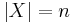 , the Shapley index for every
, the Shapley index for every 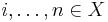 is:
is:
The Shapley value is the vector 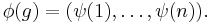
See also
References
- ^ Gustave Choquet (1953). "Theory of Capacities". Annales de l'Institut Fourier 5: 131–295.
- ^ M. Sugeno (1974). "Theory of fuzzy integrals and its applications. Ph.D. thesis". Tokyo Institute of Technology, Tokyo, Japan.
- ^ M. Grabisch (1997). "k-order additive discrete fuzzy measures and their representation". Fuzzy Sets and Systems 92 (2): 167–189. doi:10.1016/S0165-0114(97)00168-1.
- ^ H. Tahani and J. Keller (1990). "Information Fusion in Computer Vision Using the Fuzzy Integral". IEEE Transactions on Systems, Man and Cybernetic 20 (3): 733–741. doi:10.1109/21.57289.
- Beliakov, Pradera and Calvo, Aggregation Functions: A Guide for Practitioners, Springer, New York 2007.
- Wang, Zhenyuan, and, George J. Klir, Fuzzy Measure Theory, Plenum Press, New York, 1991.
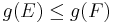 .
.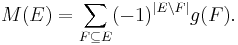
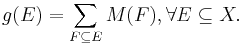
![\phi (i) = \sum_{E \subseteq X \backslash \{i\}} \frac{(n-|E|-1)!|E|!}{n!} [g(E \cup \{i\}) - g(E)].](/2012-wikipedia_en_all_nopic_01_2012/I/64f98e14a3a22af2b43d7561d4acdb46.png)